by R. Grothmann
This notebook demonstrates analytic geometry in Euler, numerically in the Euler matrix language, and in symbolic form using Maxima.
The geometry functions are in an Euler file geometry.e.
>load geometry
Numerical and symbolic geometry.
We set the range for our plot. The plots of geometry objects all hold the old plot and add the objects to it.
>setPlotRange(-0.5,2.5,-0.5,2.5);
Now set three points and plot them.
>A=[1,0]; plotPoint(A,"A"); >B=[0,1]; plotPoint(B,"B"); >C=[2,2]; plotPoint(C,"C");
Then three segments.
>plotSegment(A,B,"c"); >plotSegment(B,C,"a"); >plotSegment(C,A,"b");
The geometry functions include functions to create lines and circles. The format for the line is [a,b,c], which represents the line with equation ax+by=c.
>lineThrough(B,C)
[-1, 2, 2]
Compute the perpendicular line through A on BC.
>ha=perpendicular(A,lineThrough(B,C));
And its intersection with BC.
>H=lineIntersection(ha,lineThrough(B,C));
Plot that.
>plotPoint(H,value=1); >plotSegment(A,H):
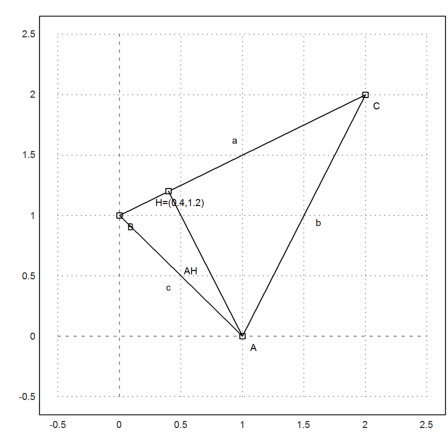
Compute the area of ABC.
>norm(A-H)*norm(B-C)/2
1.5
Compare with determinant formula.
>areaTriangle(A,B,C)
1.5
The length of the height.
>distance(A,H)
1.3416407865
The angle at C.
>degprint(computeAngle(B,C,A))
36°52'11.63''
Now the circumcircle of the triangle.
>c=circleThrough(A,B,C); getCircleRadius(c)
1.17851130198
>plotPoint(getCircleCenter(c),"U"); >plotCircle(c,"Circumcircle"):
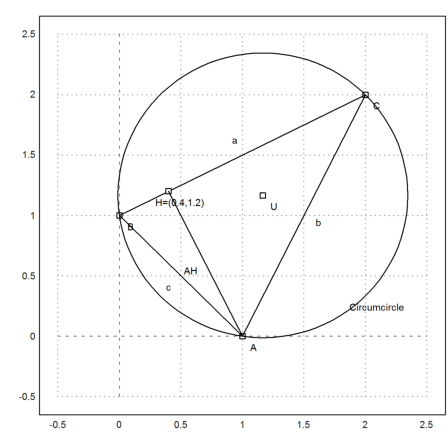
This the midpoint of the circle.
>fracformat; getCircleCenter(c), longformat;
[7/6, 7/6]
Now we compute the intersection of two angle bisectors, which is the center of the inscribed circle.
>l=angleBisector(A,C,B); g=angleBisector(C,A,B); >IP=lineIntersection(l,g)
[0.860379610028, 0.860379610028]
Add everything to the plot.
>color(5); plotLine(l); plotLine(g); color(1); >plotPoint(IP,"I"); >plotCircle(circleWithCenter(IP,norm(IP-projectToLine(IP,lineThrough(A,B))))):
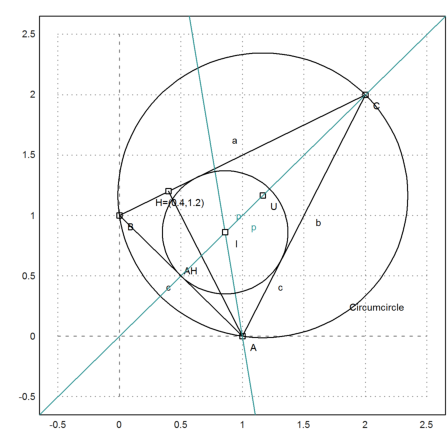
We can compute exact and symbolic geometry using Maxima.
The file geometry.e provides the same (and more) functions in Maxima. However, we can use symbolic computations now.
>A &= [1,0]; B &= [0,1]; C &= [2,2];
The functions for lines and circle work just like the Euler functions, but provide symbolic computations.
>c &= lineThrough(B,C)
[- 1, 2, 2]
We can get the equation for a line easily.
>&getLineEquation(c,x,y), &solve(%,y) | expand
2 y - x = 2
x
[y = - + 1]
2
>&getLineEquation(lineThrough(A,[x1,y1]),x,y)
(x1 - 1) y - x y1 = - y1
>ha &= perpendicular(A,lineThrough(B,C))
[2, 1, 2]
>H &= lineIntersection(c,ha)
2 6
[-, -]
5 5
>&projectToLine(A,lineThrough(B,C))
2 6
[-, -]
5 5
>&distance(A,H)
3
-------
sqrt(5)
>cc &= circleThrough(A,B,C)
7 7 5
[-, -, ---------]
6 6 3 sqrt(2)
>&getCircleRadius(cc)|float
1.178511301977579
>&computeAngle(A,C,B)
4
acos(-)
5
>&solve(getLineEquation(angleBisector(A,C,B),x,y),y)[1]
y = x
>IP &= lineIntersection(angleBisector(A,C,B),angleBisector(C,B,A))
sqrt(2) sqrt(5) + 2 sqrt(2) sqrt(5) + 2
[-------------------, -------------------]
6 6
>IP()
[0.860379610028, 0.860379610028]
Of course, we can also intersect lines with circles, and circles with circles.
>A &:= [1,0]; c=circleWithCenter(A,4); >B &:= [1,2]; C &:= [2,1]; l=lineThrough(B,C); >setPlotRange(5); plotCircle(c); plotLine(l);
The intersection of a line with a circle returns two points and the number of intersection points.
>{P1,P2,f}=lineCircleIntersections(l,c);
>P1, P2,
[4.64575131106, -1.64575131106] [-0.645751311065, 3.64575131106]
>plotPoint(P1); plotPoint(P2):
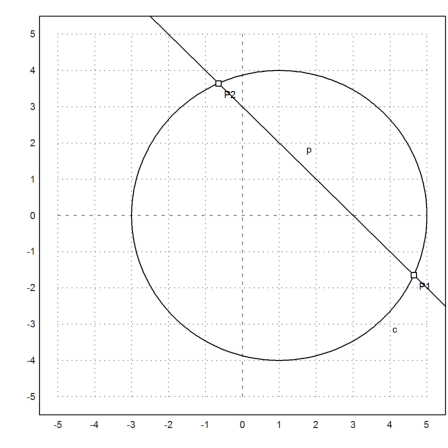
The same in Maxima.
>c &= circleWithCenter(A,4)
[1, 0, 4]
>l &= lineThrough(B,C)
[1, 1, 3]
>&lineCircleIntersections(l,c) | radcan,
[[sqrt(7) + 2, 1 - sqrt(7)], [2 - sqrt(7), sqrt(7) + 1]]
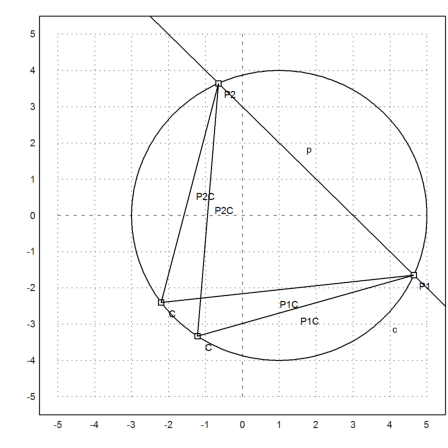
Now we check the chord angle theorem.
>C=A+normalize([-2,-3])*4; plotPoint(C); plotSegment(P1,C); plotSegment(P2,C); >computeAngle(P1,C,P2)
1.20942920289
>C=A+normalize([-4,-3])*4; plotPoint(C); plotSegment(P1,C); plotSegment(P2,C); >computeAngle(P1,C,P2)
1.20942920289
>insimg;
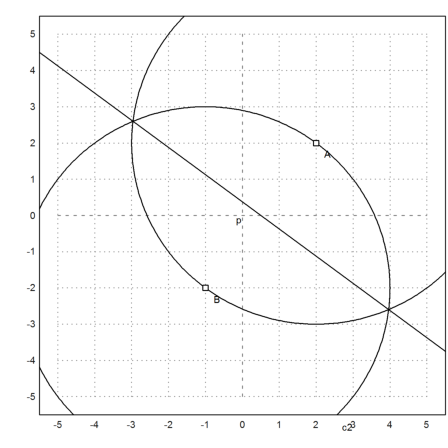
Let us construct the middle perpendicular the usual way.
>A=[2,2]; B=[-1,-2];
>c1=circleWithCenter(A,distance(A,B));
>c2=circleWithCenter(B,distance(A,B));
>{P1,P2,f}=circleCircleIntersections(c1,c2);
>l=lineThrough(P1,P2);
>setPlotRange(5); plotCircle(c1); plotCircle(c2);
>plotPoint(A); plotPoint(B); plotLine(l):
Next, we do the same in Maxima with general coordinates.
>A &= [a1,a2]; B &= [b1,b2]; >c1 &= circleWithCenter(A,distance(A,B)); >c2 &= circleWithCenter(B,distance(A,B)); >is &= circleCircleIntersections(c1,c2); P1 &= is[1]; P2 &= is[2];
The equations for the intersections are quite involved. But we can simplify, if we solve for y.
>&solve(getLineEquation(lineThrough(P1,P2),x,y),y)
2 2 2 2
- (2 b1 - 2 a1) x + b2 + b1 - a2 - a1
[y = -----------------------------------------]
2 b2 - 2 a2
This is indeed the same as the middle perpendicular, which is computed in a completely different way.
>&solve(getLineEquation(middlePerpendicular(A,B),x,y),y)
2 2 2 2
- (2 b1 - 2 a1) x + b2 + b1 - a2 - a1
[y = -----------------------------------------]
2 b2 - 2 a2